In the following screencast I show how to use conditional formatting in Excel to automatically create horizontal lines between different groups of data in a table. When applying conditional formatting you need to pay particular attention to properly setting up the cell references (absolute, relative, or mixed) in the conditional formatting formula.
The main aim of the Handbook is to provide builders of composite indicators with a set of recommendations on how to design, develop and disseminate a composite indicator. In fact, methodological issues need to be addressed transparently prior to the construction and use of composite indicators in order to avoid data manipulation and misrepresentation. In particular, to guide constructors and users by highlighting the technical problems and common pitfalls to be avoided, the first part of the Handbook discusses the following steps in the construction of composite indicators:
• Theoretical framework. A theoretical framework should be developed to provide the basis for the selection and combination of single indicators into a meaningful composite indicator under a fitness-for-purpose principle.
• Data selection. Indicators should be selected on the basis of their analytical soundness, measurability, country coverage, relevance to the phenomenon being measured and relationship to each other. The use of proxy variables should be considered when data are scarce.
• Imputation of missing data. Consideration should be given to different approaches for imputing missing values. Extreme values should be examined as they can become unintended benchmarks.
• Multivariate analysis. An exploratory analysis should investigate the overall structure of the indicators, assess the suitability of the data set and explain the methodological choices, e.g. weighting, aggregation.
• Normalisation. Indicators should be normalised to render them comparable. Attention needs to be paid to extreme values as they may influence subsequent steps in the process of building a composite indicator. Skewed data should also be identified and accounted for.
• Weighting and aggregation. Indicators should be aggregated and weighted according to the underlying theoretical framework. Correlation and compensability issues among indicators need to considered and either be corrected for or treated as features of the phenomenon that need to retained in the analysis.
• Robustness and sensitivity. Analysis should be undertaken to assess the robustness of the composite indicator in terms of, e.g., the mechanism for including or excluding single indicators, the normalisation scheme, the imputation of missing data, the choice of weights and the aggregation method.
• Back to the real data. Composite indicators should be transparent and fit to be decomposed into their underlying indicators or values.
• Links to other variables. Attempts should be made to correlate the composite indicator with other published indicators, as well as to identify linkages through regressions.
• Presentation and Visualisation. Composite indicators can be visualised or presented in a number of different ways, which can influence their interpretation.
The above list is from the Handbook on Constructing Composite Indicators: Methodology and User guide. It is published by the OECD and the Joint Research Centre of the European Commission, and it is available for download from the OECD website.
One thing researchers should keep in mind is that graphs in research reports or articles, and even those shown in verbal presentations, are not meant for the author, but for the reader or the seminar audience. The line chart that a researcher uses in the data exploration phase—with default gridlines, tick marks, and colors—may not be the one that will best communicate the researcher’s ideas to others.
The winter 2014 edition of the Journal of Economic Perspectives has a great discussion of graphing statistical data by Jonathan Schwabish of the Congressional Budget Office. He presents three principles: show the data, reduce the clutter, and integrate the text and the graph. He then works through a series of examples applying these three principles to previously published graphs (using Excel). You can download the article from here: Schwabish, Jonathan A. 2014. “An Economist’s Guide to Visualizing Data.” Journal of Economic Perspectives, 28(1): 209-34.
PivotTables are one of the most useful tools in Excel. One feature that can be confusing to use is calculated fields. In this example I show how to use calculated fields to calculate the percentage of sales arising from a specific product by city and have the percentage of sales automatically aggregate to the provincial level. The screenshots are from Excel 2007.
Here’s what the raw data looks like (Sample_Data)
The pivot table is setup as follows:
Next we add a calculated field:
We then define how the new field will be calculated. In this case we’ll call the new field “Percent Sales Product A” and define it as sales of Product A/Total Sales.
Finally we format the calculated field, and we can also drop in the province field to demonstrate that the aggregation works properly.
Credit: ©iStockphoto.com/faberfoto_it
In the opening chapter of Picturing the Uncertain World: How to Understand, Communicate, and Control Uncertainty through Graphical Display, Howard Wainer writes about what he calls The Most Dangerous Equation: the equation for the standard error of the mean which he refers to as DeMoivre’s equation. Wainer’s general point is that there is greater variability in small samples. He gives several examples demonstrating this phenomenon: U.S. counties with the lowest and highest age adjusted kidney cancer rates “tend to be very rural, midwestern, southern, and western counties”; the highest and lowest performing schools tend to be smaller schools; and the safest and most dangerous cities in the U.S. tend to be smaller cities. Failing to take into account the effect of the sample size on a statistic is a cognitive bias called insensitivity to sample size. From Wikipedia:
Insensitivity to sample size is a cognitive bias that occurs when people judge the probability of obtaining a sample statistic without respect to the sample size. For example, in one study subjects assigned the same probability to the likelihood of obtaining a mean height of above six feet [183 cm] in samples of 10, 100, and 1,000 men. In other words, variation is more likely in smaller samples, but people may not expect this.
In another example, Amos Tversky and Daniel Kahneman asked subjects:
A certain town is served by two hospitals. In the larger hospital about 45 babies are born each day, and in the smaller hospital about 15 babies are born each day. As you know, about 50% of all babies are boys. However, the exact percentage varies from day to day. Sometimes it may be higher than 50%, sometimes lower. For a period of 1 year, each hospital recorded the days on which more than 60% of the babies born were boys. Which hospital do you think recorded more such days?
1. The larger hospital
2. The smaller hospital
3. About the same (that is, within 5% of each other)
56% of subjects chose option 3, and 22% of subjects respectively chose options 1 or 2. However, according to sampling theory the larger hospital is much more likely to report a sex ratio close to 50% on a given day than the smaller hospital.
This phenomenon—that smaller units (hospitals, cities, schools, etc.) have more random variability—is important to take into account when ranking or comparing performance indicators as part of a performance measurement system. David Spiegelhalter, a statistician at the University of Cambridge, introduced the use of funnel plots to compare performance indicators in his 2005 article, Funnel plots for comparing institutional performance. A funnel plot is a scatter plot of the actual values of a particular performance indicator for each unit (i.e., each city, school, hospital, etc) on the y-axis against the sample size on the x-axis along with a horizontal line showing the overall value of the performance indicator and control limits around the overall value. Units that lie outside the control limits have performance that is significantly different than the overall value. Recently on his blog, Understanding Uncertainty, Spiegelhalter worked through an example of using a funnel plot to compare the performance of local governments in England for the following performance indicator: the proportion of children whose adoption placement occurred within 12 months. He found that the performance for the majority of local governments was within the control limits and “so their variation [was] essentially indistinguishable from chance.”
Funnel plots are a very useful tool when measuring differences in performance. From the article, Statistical Process Control Methods in Public Health Intelligence:
Methods based on ranking, such as league tables or percentiles, have a number of flaws. The main problem with ranking is the implicit assumption that apparent differences between organisations are the results of better or poorer performance. Simply because institutions may produce different values for an indicator, and we naturally tend to rank these values, does not mean that we are observing variation in performance. All systems within which institutions operate, no matter how stable, will produce variable outcomes.
The questions we need to answer are: ‘Is the observed variation more or less than we would normally expect?’; ‘Are there genuine outliers?’; ‘Are there exceptionally good performers?’; ‘What reasons might there be for excess variation’, and so on. Alternative methods [to ranking] based on understanding variation [such as funnel plots] may be more appropriate…
Fortunately, it’s fairly straightforward to make funnel plots: here’s how in Excel, Stata, and SAS.
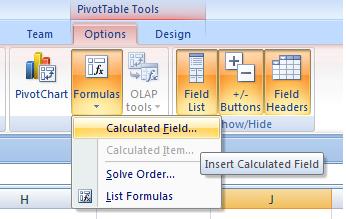
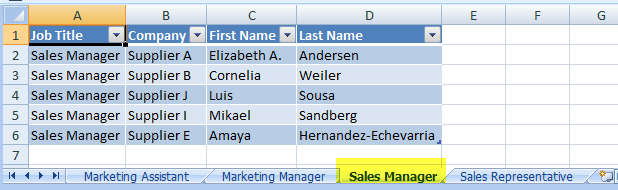
Credit: ©iStockphoto.com/3d_kot
Coding categorical data (such as male/female or geographic region) as dummy variables is probably the most common way of incorporating qualitative data into a regression equation. Under dummy variable coding, the coefficient on a dummy variable in a regression equation is the difference between the average value of the outcome variable for the category that is included and the average value of the base category (the category that is excluded). Dummy variable coding isn’t the only way to incorporate categorical variables into a regression equation. Another coding scheme is called effect coding. Under effect coding, the coefficient on the included category is the difference between the average value of the outcome variable for the included category and the overall average value of the outcome variable.
In the following examples illustrating the difference between the two coding schemes, the outcome variable is starting salary and the independent variable is either male or female.
Here is the dummy variable approach:
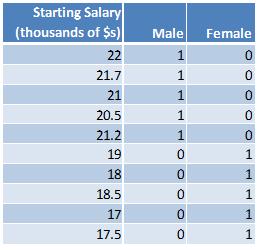
Here are the summary statistics:
Average value of starting salary for everyone: (22+21.7+21+20.5+21.2+19+18+18.5+17+17.5)/10 = 19.64
Average value of starting salary for males: (22+21.7+21+20.5+21.2)/5 = 21.28
Average value of starting salary for females: (19+18+18.5+17+17.5)/5 = 18
The difference between the average value of salaries for males and females: (21.28-18) = 3.28
The difference between the average value of salaries for females and males: (18-21.28) = -3.28
The difference between the average salary for males and the overall average salary: (21.28-19.64) = 1.64
The difference between the average salary for females and the overall average salary: (18-19.64) = -1.64
Here are the results from running the regression where the outcome variable is starting salary and the independent variable is male:
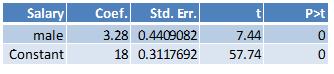
The value of the coefficient on the male dummy, 3.28, is the difference between the average value of the starting salary between males and females. The constant, 18, is the average value of the starting salary for females (the base category).
Here are the results from running the regression where the outcome variable is starting salary and the independent variable is female:
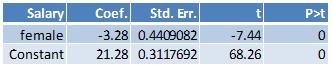
The value of the coefficient on the female dummy, -3.28, is the difference between the average value of the starting salary between females and males. The constant, 21.28, is the average value of the starting salary for males (the base category).
Under the effect coding scheme, the categorical variables are coded in such a way that the values for each categorical value sum to zero. In the simplest case where there is an equal number of observations for each category, the value of the excluded category is set to negative 1. Here is what the above data look like under the effect coding scheme:
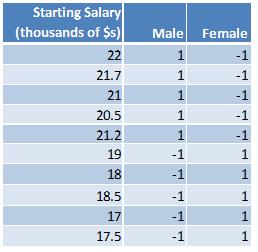
Notice that the sum of the values for male (1+1+1+1+1+(-1)+(-1)+(-1)+(-1)+(-1)) is zero and that the sum of the values for female ((-1)+(-1)+(-1)+(-1)+(-1)+1+1+1+1+1) is also zero.
The summary statistics are the same as before:
Average value of starting salary for everyone: (22+21.7+21+20.5+21.2+19+18+18.5+17+17.5)/10 = 19.64
Average value of starting salary for males: (22+21.7+21+20.5+21.2)/5 = 21.28
Average value of starting salary for females: (19+18+18.5+17+17.5)/5 = 18
The difference between the average value of salaries for males and females: (21.28-18) = 3.28
The difference between the average value of salaries for females and males: (18-21.28) = -3.28
The difference between the average salary for males and the overall average salary: (21.28-19.64) = 1.64
The difference between the average salary for females and the overall average salary: (18-19.64) = -1.64
Here are the results from running the regression where the outcome variable is starting salary and the independent variable is male:
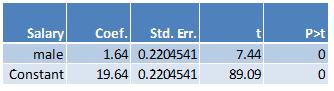
The value of the coefficient on the male dummy, 1.64, is the difference between the average value of the starting salary for males and the overall average salary. The constant, 19.64, is the average value of the overall starting salary.
Here are the results from running the regression where the outcome variable is starting salary and the independent variable is female:
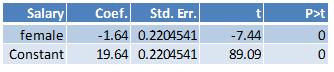
The value of the coefficient on the female dummy, -1.64, is the difference between the average value of the starting salary for females and the overall average salary. The constant, 19.64, is the average value of the overall starting salary.
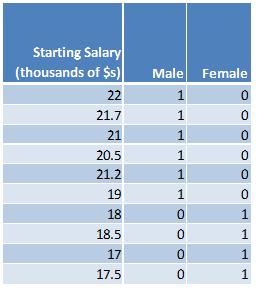
In the above examples, there are five males and five females. When there an equal number of observations, the categories are said to be balanced. When the categories have different numbers of observations, the categories are said to be unbalanced. When the categories are unbalanced, the values for the categorical variables can be calculated as follows so that they will sum to zero: determine the proportion of cases each group makes up of the total and then divide the proportion for each group by negative one times the proportion of cases that belong to the base category. Suppose there are six males and four females and the data are as follows:
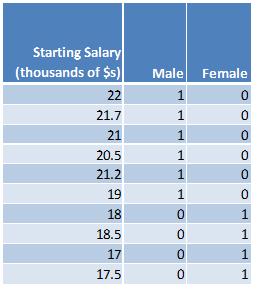
Here are the summary statistics:
Average value of starting salary for everyone: (22+21.7+21+20.5+21.2+19+18+18.5+17+17.5)/10 = 19.64
Average value of starting salary for males: (22+21.7+21+20.5+21.2+19)/6 = 20.9
Average value of starting salary for females: (18+18.5+17+17.5)/4 = 17.75
The difference between the average value of salaries for males and females: (20.9-17.75) = 3.15
The difference between the average value of salaries for females and males: (17.75-20.9) = -3.15
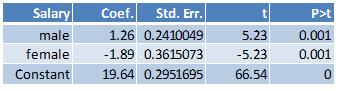
The difference between the average salary for males and the overall average salary: (20.9-19.64) = 1.26
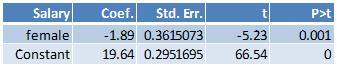
The difference between the average salary for females and the overall average salary: (18-19.64) = -1.89
In the above example, there are six males and four females and therefore the proportion of males is 0.6 and the proportion of females is 0.4. Under the effect coding scheme, the value for the male variable will be (-1)*(.06)/(0.4) = -1.5. The value for the female variable will be (-1)*(0.4)/(0.6) = -0.666666667. The effect coded data will look as follows:
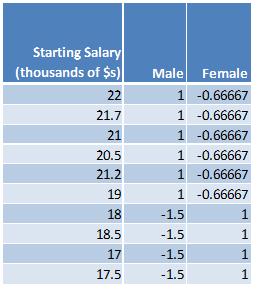
Notice that the sum of the values for male (1+1+1+1+1+1+(-1.5)+(-1.5)+ (-1.5)+ (-1.5)) is zero and that the sum of the values for female ((-2/3)+(-2/3)+(-2/3)+(-2/3)+(-2/3)+(-2/3)+1+1+1+1) is also zero.
Here are the results from running the regression with dummy variable coding where the outcome variable is starting salary and the independent variable is male:
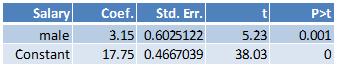
Here are the results from running the regression with dummy variable coding where the outcome variable is starting salary and the independent variable is female:
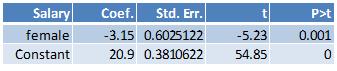
Here are the results from running the regression with effect variable coding where the outcome variable is starting salary and the independent variable is male:
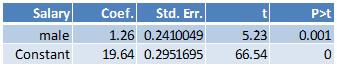
Here are the results from running the regression with effect variable coding where the outcome variable is starting salary and the independent variable is female:
The results from effect coding are equivalent to constrained linear regression with dummy variable coding where the constraint is that the sum of the proportion of each categorical variable sum to zero. Here’s an example illustrating the constrained regression approach. The data is coded using the dummy variable coding scheme.
Since there are six males and four females, the following constraint is placed on the regression equation: (0.6)*male + (0.4)*female = 0. The regression equation is starting salary = constant + male + female.
In Stata this is accomplished with the following two commands:
constraint define 1 0.6*male + 0.4*female = 0
cnsreg salary male female, constraint(1)
Here are the results from estimating the constrained regression equation:
References:
Additional coding systems for categorical variables in regression analysis; The Institute for Digital Research and Education, UCLA.
Basic Econometrics, 3rd edition by Damodar Gujarati; The above sample data is from page 501 of the text book.
Coding Categorical Variables in Regression Models: Dummy and Effect Coding (StatNews #72); Cornell Statistical Consulting Unit.
Coding Schemes for the Religion and Life Satisfaction Example; Jason Newsom.
Dummy Variables: Mechanics v. Interpretation; Daniel B Suits; The Review of Economics and Statistics, 1984, vol. 66, issue 1, pages 177-80.
Interpreting Dummy variables; Peter Kennedy; The Review of Economics and Statistics, 1986, vol. 68, issue 1, pages 174-75.
Credit: ©iStockphoto.com/Inhabitant
If you’re looking for data sets for testing purposes, you may find the UC Irvine Machine Learning Repository useful. It has over 200 data sets available for download.
Demetra+ is a free program provided by Eurostat and the National Bank of Belgium. The software provides a full set of tools for testing whether seasonality exists and then adjusting for it using either the X-12-ARIMA or the TRAMO/SEATS methods.
Links:
Download Demetra+ (the older version of the program)
Demetra+ User manual (PDF)
The Practical Guide to seasonal adjustment with Demetra+ (PDF) by the United Nations Economic Commission for Europe
Credit: ©iStockphoto.com/meckimac
Here’s some data in Excel 2007 copied from the Northwind Traders database that comes with Microsoft Access.
In this post, I’ll cover how to create separate worksheets that only show the information for people having a specific job title.
The final result will look like this:
This can easily be accomplished in a few steps with some VBA code.
1. Make a pivot table on a new worksheet with Job Title as the Report Filter and Company Name as what’s being counted.
2. Rename the worksheet with the pivot table on it as “main data”.
3. Run the following VBA code. This is based on code originally from Debra Dalgleish.
Sub ExpandPivot()
Dim pt As PivotTable
Dim pf As PivotField
Dim pi As PivotItem
Set pt = Sheets("main data").PivotTables.Item(1)
For Each pf In pt.PageFields
For Each pi In pf.PivotItems
pt.PivotFields(pf.Name).CurrentPage = pi.Name
Range("A4").Select
Selection.ShowDetail = True
Sheets("main data").Select
Next
Next pf
End Sub
4. After running the above code, you’ll have separate worksheets with only the data for each job title. The new worksheets will have generic names such as “Sheet5”. These new sheets can easily be given new names based on the job title.
4a. Delete the worksheet with the pivot table (i.e., the “main data” sheet), the source worksheet which has data on all job titles, and any blank sheets in the workbook. The workbook should only have the newly created worksheets.
4b. Run the following code (based on code from here) to rename the worksheets:
Sub ReNameWorksheets()
For Each sht In ThisWorkbook.Worksheets
sht.Name = sht.Range("A2")
sht.Activate
Cells.EntireColumn.AutoFit
Range("A1").Select
Next sht
End Sub
The above code is pulling the name for each worksheet from the value in cell A2. The one thing you’ll need to watch out for is values that violate the rules for worksheet names in Excel. A worksheet name can be at most 31 characters and can’t have any of the following characters: \ / ? *[]
From the Wikipedia article on Brooks’ law:
Brooks’ law is a principle in software development which says that “adding manpower to a late software project makes it later”. It was coined by Fred Brooks in his 1975 book The Mythical Man-Month. The corollary of Brooks’ Law is that there is an incremental person who, when added to a project, makes it take more, not less time.
. . .
Brooks points to two main factors that explain why it works this way:
1. It takes some time for the people added to a project to become productive. Brooks calls this the “ramp up” time. Software projects are complex engineering endeavors, and new workers on the project must first become educated about the work that has preceded them; this education requires diverting resources already working on the project, temporarily diminishing their productivity while the new workers are not yet contributing meaningfully. Each new worker also needs to integrate with a team composed of multiple engineers who must educate the new worker in their area of expertise in the code base, day by day. In addition to reducing the contribution of experienced workers (because of the need to train), new workers may even have negative contributions – for example, if they introduce bugs that move the project further from completion.
2. Communication overheads increase as the number of people increases. The number of different communication channels increases along with the square of the number of people; doubling the number of people results in four times as many different conversations. Everyone working on the same task needs to keep in sync, so as more people are added they spend more time trying to find out what everyone else is doing.
